rsbench: A Neuro-Symbolic Benchmark Suite for Concept Quality and Reasoning Shortcuts

Samuele Bortolotti¹, Emanuele Marconato^2,1, Tommaso Carraro^3,6, Paolo Morettin¹,
Emile van Krieken⁴, Antonio Vergari⁴, Stefano Teso^5,1, Andrea Passerini¹

¹DISI, University of Trento, ²University of Pisa, ³Fondazione Bruno Kessler, ⁴University of Edinburgh,
⁵CIMeC, University of Trento, ⁶University of Padova

Abstract

The advent of powerful neural classifiers has increased interest in problems that require both learning and reasoning. These problems are critical for understanding important properties of models, such as trustworthiness, generalization, interpretability, and compliance to safety and structural constraints. However, recent research observed that tasks requiring both learning and reasoning on background knowledge often suffer from reasoning shortcuts (RSs): predictors can solve the downstream reasoning task without associating the correct concepts to the high-dimensional data. To address this issue, we introduce rsbench, a comprehensive benchmark suite designed to systematically evaluate the impact of RSs on models by providing easy access to highly customizable tasks affected by RSs. Furthermore, rsbenchimplements common metrics for evaluating concept quality and introduces novel formal verification procedures for assessing the presence of RSs in learning tasks. Using rsbench, we highlight that obtaining high quality concepts in both purely neural and neuro-symbolic models is a far-from-solved problem.

Downloads

Data: GDrive, Zenodo

Codebase: GitHub

Paper: OpenReview

What is a Reasoning Shortcut?

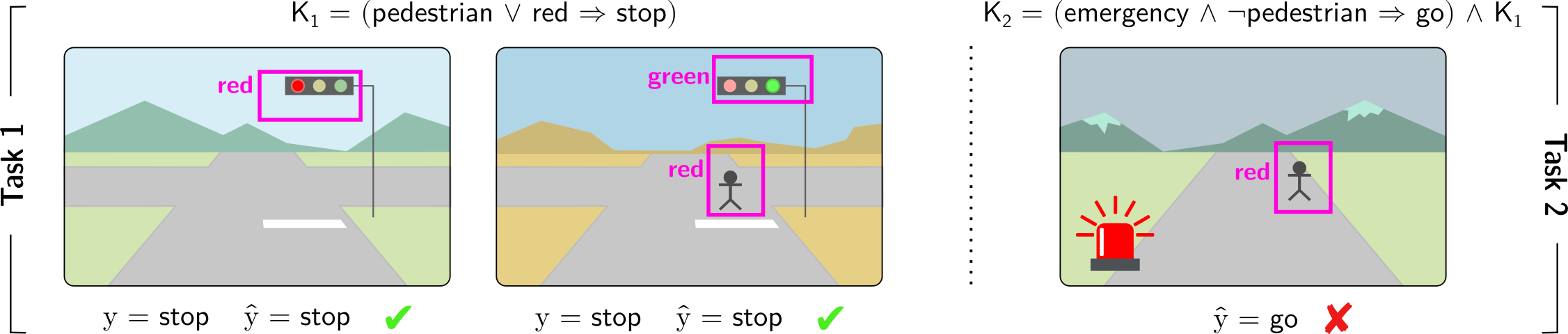
What are L&R tasks? In learning and reasoning tasks, machine learning models should predict labels that comply with prior knowledge. For instance, in autonomous vehicle scenario, the model should predict stop or go based on what obstacles are visible in front of the vehicle, and the prior knowledge encodes the rule that if a pedestrian or a red_light is visible then it should definitely predict stop.

What is a reasoning shortcut? A RS occurs when the model predicts the right label by inferring the wrong concepts. For instance, it might confuse pedestrians for red_lights as both entail the same (correct) stop action.

What are the consequences? RSs can compromise the interpretability of model explanations (e.g., these might show that a prediction depends on the red_lights present in the image, while in reality it depends on pedestrians!) and generalization to out-of-distribution tasks (e.g., if a vehicle is authorized to cross over red_lights in the case of an emergency, and it confuses these with pedestrians, this might lead to harmful decisions).

Image taken with permission from: Marconato et al. “Not all neuro-symbolic concepts are created equal: Analysis and mitigation of reasoning shortcuts.” NeurIPS 2023.

Overview

• A Variety of L&R Tasks: rsbenchoffers five L&R tasks and at least one data set each. The tasks come in different flavors – arithmetic, logic, and high-stakes – and with a formal specification of the corresponding prior knowledge. rsbenchalso provides data generators for creating new OOD splits useful for testing the down-stream consequences of RSs.

• Evaluation: rsbenchcomes with implementations for several metrics for evaluating the quality of label and concept predictions, as well as visualization code for them.

• Verification: rsbenchimplements a new algorithm, countrss, that makes use of automated reasoning packages for formally veryfing whether a L&R task allows for RSs without training any model! This tool works with any prior knowledge encoded in CNF format, the de-facto standard in automated reasoning.

• Example code: our repository comes with example code for training and evaluating a selection of state-of-the-art machine learning architectures, including Neuro-Symbolic models, Concept-bottleneck models, and regular neural networks.

Usage

In this section we provide useful infromation to get started with rsbench.

Configure and run the data generators

The data generators are available at the following GitHub link.

The datasets included are:

• MNMath
• MNLogic
• Kand-Logic
• CLE4EVR
• SDD-OIA

Each generator is highly customizable through configuration files. For MNMath, MNLogic, and Kand-Logic, you need to edit a .yml file, with examples and instructions available in the examples_config folder. On the other hand, CLE4EVR and SDD-OIA use .json configuration files. For further details, please refer to the respective GitHub page for each generator.

Load rsbench data and train your model

To load and use rsbenchdata, you can use the provided suite that comprises data loading, model training, and evaluation. This ready-to-use toolkit is available at this GitHub link. Alternatively, you can create your own dataset class by writing just a few lines of code

from rss.datasets.xor import MNLOGIC

class required_args:
    def __init__(self):
      self.c_sup = 0 # specifies % supervision available on concepts
      self.which_c = -1 # specifies which concepts to supervise, -1=all
      self.batch_size = 64 # batch size of the loaders

args = required_args()

dataset = MNLOGIC(args)
train_loader, val_loader, test_loader = dataset.get_loaders()

model = #define your model here
optimizer = #define optimizer here
criterion = #define loss function here

for epoch in range(30):
    for images, labels, concepts in train_loader:
        optimizer.zero_grad()
        outputs = model(images)
        loss = criterion(outputs, labels, concepts)
        loss.backward()
        optimizer.step()

Quickstart

We provide a simple tutorial designed to demonstrate how to load and use the data generated by rsbench. This tutorial is meant to give a quick overview and get you started with the data we provide. You can access the Google Colab tutorial using the following link:

MNIST Math Google Colab

The example data used in the tutorial is MNISTMath. You can easily create and customize the task you want using our data generator. Once you have created your dataset, you can upload the zip file to your Google Drive and follow the tutorial to try it out.

Evaluation

For a more thorough evaluation of the model, we recommend exploring the rsseval folder in our code repository, which you can find here:

rsseval

Within this folder, you’ll find a notebook dedicated to evaluating concept quality using the metrics discussed in our paper. This will help you assess the performance and quality of the models more comprehensively.

MNMath

MNMath is a novel multi-label extension of MNIST-Addition Manhaeve et al., 2018 in which the goal is to predict the result of a system of equations of MNIST digits. The input image is the concatentation of all MNIST digits appearing in the system, and the output is a vector with as many elements as equations. Models trained on this task can learn to systematically extract the wrong digits from the input image.

An example RS: For the (linear) system in the example above, a model can confuse 3’s with 4’s and still perfectly predict the output of the system. However, for a new, out-of-distribution task like $2 + 4$, it will wrongly output $5$.

Ready-made: MNAdd-Half is a modified version of MNIST-Addition that focuses on only half of the digits, specifically those from 0 to 4. It was introduced for the first time in Marconato et al., 2024b.

The dataset includes the following combinations of digits:

+ = 0

+ = 1

+ = 5

+ = 6

The digits 0 and 1 are unaffected by reasoning shortcuts, while digits 2, 3, and 4 can be predicted in various ways, as illustrated below.

The MNAdd-Half dataset contains a total of 2940 fully annotated training samples, 840 validation samples, 420 test samples, and an additional 1080 out-of-distribution test samples. These samples exclusively consist of sums involving these digits, such as 1 + 3 = 4.

There are three potential optimal solutions, two of which are reasoning shortcuts. Specifically:

→ 0, → 1, → 2, → 3, → 4

→ 0, → 1, → 3, → 2, → 3

→ 0, → 1, → 4, → 1, → 2

Ready-made: MNAdd-EvenOdd is yet another modified version of MNIST-Addition that focuses on only some digit combinations, specifically combinations of either even or odd digits. It was first introduced in Marconato et al., 2023.

+ = 6
+ = 10
+ = 10
+ = 12

+ = 6
+ = 10
+ = 10
+ = 12

It contains 6720 fully annotated training samples, 1920 validation samples, and 960 in-distribution test samples, along with 5040 out-of-distribution test samples representing all other sums not seen during training.

As described in Marconato et al., 2024a, the number of deterministic reasoning shortcuts is determined by finding integer solutions for the digits in the linear system, totaling 49.

An example of RS in this setting is the following:

→ 5, → 5, → 7, → 7, → 9, → 1, → 1, → 3, → 3, → 5

MNLogic

RSs arise whenever the knowledge $\mathsf K$ allows deducing the right label from multiple configurations of concepts. This form of non-injectivity is a standard feature of most logic formulas, and in fact formulas as simple as the XOR are riddled by RSs. MNLogic allows to probe the pervasiveness of RSs in random logic formulas. Specifically, the input image is the concatenation of $k$ MNIST images of zeros and ones representing the truth value of $k$ bits, and the ground-truth label $y$ is whether they satisfies the formula or not.

By default, the MNLogic assumes the formula is a $k$-bit XOR, but any other formula can be supplied. rsbenchprovides code to generate random CNF formulas, that is, random conjunctions of disjunctions (clauses) of $k$ bits. The code allows to control the number of bits $k$ and the number of structure of the random formula, that is, the number of clauses and their length. It also avoids trivial data by ensuring each clauses is neither a tautology nor a contradiction.

Kand-Logic

This task, inspired by Wassily Kandinsky’s paintings and Mueller and Holzinger 2021 requires simple (but non-trivial) perceptual processing and relatively complex reasoning in classifying logical patterns on sets of images comprising different shapes and colors. For example, each input can comprise two $64 \times 64$ images, i.e., $x = (x_1, x_2)$, each depicting three geometric primitives with different shapes (square, triangle, circle) and colors (red, blue, yellow). The goal is to predict whether $x_1$ and $x_2$ fit the same predefined logical pattern or not. The pattern is built out of predicates like all primitives in the image have a different color, all primitives have the same color, and exactly two primitives have the same shape.

Unlike MNLogic, in Kand-Logic each primitive has multiple attributes that cannot easily be processed separately. This means that RSs can easily appear, e.g., confuse shape with color when either is sufficient to entail the right prediction, as in the example above. We provide the data set used in Marconato et al. 2024b ($3$ images per input with $3$ primitives each) and a generator that allows configuring the number of images and primitives per input and the pattern itself.

CLE4EVR

CLE4EVR focuses on logical reasoning over three-dimensional scenes, inspired by CLEVR Johnson et al. and CLEVR-HANS Stammer et al..

Each input image $x$, of size $240 \times 320$, contains a variable number of objects differing in size ($3$ possible values), shape ($10$), color ($10$), material ($2$), position (real), and rotation (real), and the goal is to determine whether the objects satisfy a pre-specified rule that depends on all discrete attributes of the objects in the scene. Example of shapes are sphere, pyramid, and diamonds.

The default knowledge $\mathsf K$ is designed to induce Reasoning Shortcuts: it asserts that an image $x$ is positive iff at least two objects $x_i$ and $x_j$ have the same color and shape, i.e., $\exists i \ne j \ . \ ({\tt sha}(x_i) = {\tt sha}(x_j)) \land ({\tt col}(x_i) = {\tt col}(x_j))$. Reasoning Shortcuts, include confusing one shape for one another, or confusing colors for shapes and vice versa. For example, a model may associate red pyramid to gray sphere while yielding perfect task accuracy.

The generator allows to customize the number of objects per image, the knowledge, and whether occlusion is allowed.

BDD-OIA

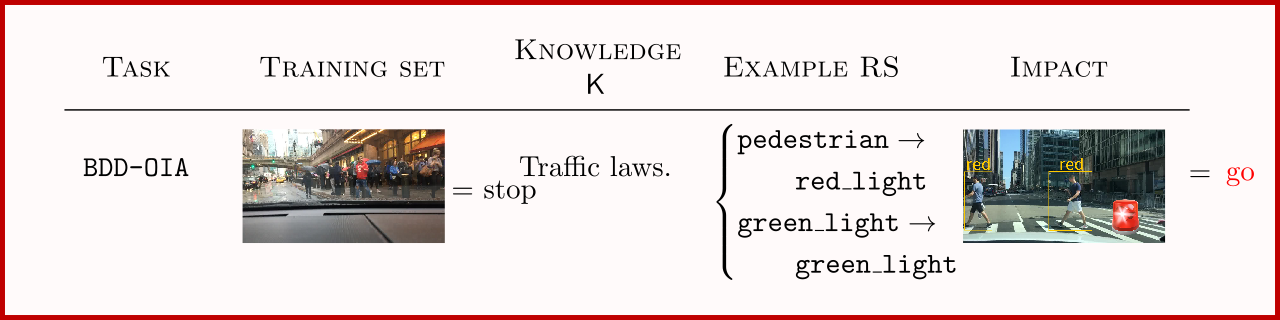
BDD-OIA Xu et al. is a multi-label autonomous driving task for studying RSs in real-world, high-stakes scenarios. The goal is to infer what actions out of ${ {\tt forward}, {\tt stop}, {\tt left}, {\tt right} }$ are safe depending on what objects (e.g., cars, traffic signs) are present in an input dashcam image.

Input images, of size $720 \times 1280$, come with concept-level annotations, making it possible to assess the quality of the learned concepts. The dataset comprises $16,082$ training examples, $2,270$ validation examples and $4,572$ test examples.

The knowledge $\mathsf K$ establishes that, e.g., it is not safe to move $\tt forward$ if there are pedestrians on the road, based on a set of $21$ binary concepts indicating the presence of different obstacles on the road. The constraints specify conditions for being able to proceed (${\tt green\_light} \lor {\tt follow} \lor {\tt clear} \Rightarrow {\tt forward}$), stop (${\tt red\_light} \lor {\tt stop\_sign} \lor {\tt obstacle} \Rightarrow {\tt stop}$), and for turning left and right, as well as relationships between actions (like ${\tt stop} \Rightarrow \lnot {\tt forward}$).

Common Reasoning Shortcuts allow to, for example confuse ${\tt pedestrians}$ with ${\tt red\_light}$ s, as they both imply the correct $ {\tt stop}$ action for all training examples.

SDD-OIA

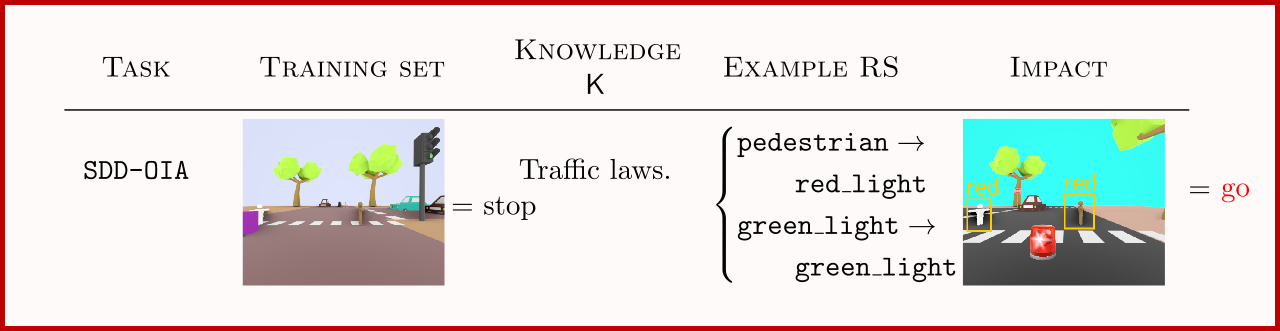
SDD-OIA is a synthetic replacement for BDD-OIA that comes with a fully configurable {data generator}, enabling fine-grained control over what labels, concepts, and images are observed and the creation of OOD splits. In short, SDD-OIA shares the same classes, concepts and (by default) knowledge as BDD-OIA, but the images are 3D traffic scenes modelled and rendered using Blender as $469 \times 387$ RGB images.

Images are generated by first sampling a desired label $\mathbf y$, then picking concepts $\mathbf c$ that yield that label, and then rendering an image $\mathbf x$ displaying those concepts. This allows to easily control what concepts and labels should appear in all data splits, which in turn determine what kinds of RSs can be learned. The dataset we propose contains overall $6820$ training examples, $1464$ validation examples, and $1464$ test examples. Reasoning Shortcuts learned in this task rensemble those in BDD-OIA.

We also include a OOD test scenario, where the knowledge changes including a new exception under emergency case, this includes in total $1000$ examples. Here, the vehicle is allowed to cross red lights in case of an ${\tt emergency}$. Formally, this alterates the label predictions where the new ${\tt emergency}$ variable that conditions the traffic rules, that is, $(\lnot {\tt emergency} \implies \text{original rule for } {\tt stop})$ $\land$ $(\lnot {\tt emergency} \implies \text{alternative rule for } {\tt stop})$, and similarly for ${\tt turn\_left}$ and ${\tt turn\_right}$.

SDD-OIA comes with its generator, allowing to test different cases and creationg variations of other OOD scenarios can be created.

Verification

count-rss is a small tool that is able to enumerate the RSs in a task by reducing the task to model counting (#SAT). In short, count-rss takes a DIMACS CNF specification of the prior knowledge and a data set, and outputs a DIMACS CNF specification of the RS counting problem, which can be fed to any #SAT solver. Due to their large number even on seemingly simple tasks, we suggest using the state-of-the-art approximate #SAT solver ApproxMC.

Generating the RSs counting encoding

Use python gen-rss-count.py for generating a DIMACS encoding of the counting task.

On small datasets/tasks, the count of RSs can be computed directly (and exactly) with the -E flag. For instance:

$ python gen-rss-count.py xor -n 3 -E

computes all the RSs resulting from the XOR task on 3 variables with exhaustive supervision.

Partial/incomplete supervision can be controlled with -d P with P in [0,1]. For instance:

$ python gen-rss-count.py xor -n 3 -E -d 0.25

computes all the RSs when only 1/4 (i.e. 2 examples) are provided. The optional --seed argument sets the seed number.

Beyond illustrative the XOR case, random CNFs with N variables, M clauses of length K can be evaluated:

$ python gen-rss-count.py random -n N -m M -k K

Custom task expressed in DIMACS format are supported, for instance:

$ python gen-rss-count.py cnf and.cnf

Use the flag -h for help on additional arguments.

Counting RSs with pyapproxmc

Once the encoding of the problem is generated with gen-rss-count.py, use:

$ python count-amc.py PATH --epsilon E --delta D

for obtaining an (epsilon,delta)-approximation of the exact RS count.

Alternative solvers can be used analogously. Exact solvers include pyeda and pysdd.

Relevant Papers using rsbench for studying RSs

• Authors: Emanuele Marconato, Stefano Teso, Antonio Vergari, Andrea Passerini
  Title: Not all neuro-symbolic concepts are created equal: analysis and mitigation of reasoning shortcuts
  Publication: Neural Information Processing Systems (NeurIPS), 2023
  TL;DR: Why RSs appear, their root causes, and mitigation strategies
• Authors: Emanuele Marconato, Samuele Bortolotti, Emile van Krieken, Antonio Vergari, Andrea Passerini, Stefano Teso
  Title: BEARS Make Neuro-Symbolic Models Aware of their Reasoning Shortcuts
  Publication: Uncertainty in Artificial Intelligence (UAI), 2024
  TL;DR: How to make Neuro-Symbolic models aware of their RSs
• Authors: Xiao-Wen Yang, Wen-Da Wei, Jie-Jing Shao, Yu-Feng Li, Zhi-Hua Zhou
  Title: Analysis for Abductive Learning and Neural-Symbolic Reasoning Shortcuts
  Publication: International Conference on Machine Learning (ICML), 2024
  TL;DR: Reduce shortcut risk using Abductive Learning

Metadata

Preliminary metadata for the datasets we provide in the Zenodo archive and Google Drive is listed here:

• bbox_kand_logic
• kand_logic_croissant
• sdd_oia
• sdd_oia_embeddings

License

Code: Most of our code is distributed under the BSD 3 license. The CLE4EVR and SDDOIA generators are derived from the CLEVR code base, which is distributed under the permissive BSD license. The Kand-Logic generator is based on the Kandinsky-patterns code, which is available under the GPL-3.0 license, and so is our generator.

Data: All ready-made data sets and generated datasets are distributed under the CC-BY-SA 4.0 license, with the exception of Kand-Logic, which is derived from Kandinsky-patterns and as such is distributed under the GPL-3.0 license.